Série alphabétique dans les tests psychotechniques, comment les surmonter

Dans cette entrée, nous parlerons en profondeur de la série alphabétique, également connue sous le nom de lettres de lettres, et qui sont largement utilisées dans les processus de sélection du personnel, les oppositions et Tests psychotechniques en général. Si vous préférez, vous pouvez également voir cette entrée vidéo.

Nous allons vous apprendre à surmonter ce type de série et nous révélerons tous ses secrets.

Nous vous recommandons de passer en revue notre vidéo de série numérique car la plupart des séries alphabétiques ne sont rien de plus qu'un cas spécifique de ceux.

La série d'alphabétisation est présentée comme un ensemble de lettres qui suivent un ordre logique que nous devrons découvrir, pour déduire la prochaine lettre de la série.

Pour résoudre ces types de questions avec facilité et minimiser les erreurs, il est très important de maîtriser l'ordre alphabétique et de connaître la position que chaque lettre occupe dans le même. Ainsi, par exemple, la lettre "A" est associée au numéro 1, car il occupe la première position de l'alphabet, la lettre "B", est associée au numéro 2 et ainsi de suite à la lettre "Z" qui occupe la position 27 dans l'alphabet espagnol. L'alphabet doit être considéré comme cycliquement, c'est-à-dire après que la lettre "z" continuerait le "A" et ainsi de suite.

Normalement, les doubles lettres: "ch", "ll" et "rr" ne sont pas considérés comme faisant partie de l'alphabet lors de la résolution de la série, bien que chaque fois que possible, il est pratique de demander à l'examinateur.

Contenu

Basculer

• Série d'alphabétisation simple
• Multiples séries d'alphabétisation entrecoupées
• Séries mixtes
• Modifications et variations
• Série littérale
• Cas spéciaux

Série d'alphabétisation simple

Ce sont la série la plus simple et celles que nous trouverons sûrement dans tout test psychotechnique. Prenons un exemple:

B d f h ?

Si nous regardons, nous pouvons voir que l'ordre alphabétique des lettres augmente progressivement.

Si nous remplaçons chaque lettre pour la valeur numérique correspondant à la position de chacun à l'intérieur de l'alphabet, la série précédente devient cet autre, que nous appellerons "Base Series":

2 4 6 8 ?

Et si nous nous souvenons de ce qu'ils ont appris dans la vidéo de la série numérique, nous verrons qu'il y a une augmentation de +2 Unités entre deux éléments de la série de base:

Nous avons donc une série arithmétique de facteur fixe (+2), de sorte que la valeur suivante de la séquence sera obtenue en ajoutant 2 au dernier élément de la série, c'est-à-dire: 8 + 2 = 10.

Maintenant, nous devons rechercher la lettre qui occupe la dixième position de l'alphabet, qui est le "J", Et c'est la bonne réponse.

Cette série est simple, mais en plus compliquée, il peut être utile d'avoir un tableau pour calculer les équivalences du numéro à la lettre et vice versa.

Nous ne pouvons pas transporter ce tableau avec nous pour faire le test, mais vous aurez probablement du papier pour faire des calculs et nous pouvons écrire le tableau d'équivalence.

Dans l'exemple que nous avons vu auparavant, la série de bases est un facteur fixe, mais nous pouvons trouver tout type de ceux que nous avons vus dans la vidéo de la série numérique: facteur fixe ou variable arithmétique, facteur géométrique fixe ou variable, puissances, etc.

Nous verrons quelques exemples de différents types pour le rendre plus clair. Essayez de résoudre la série que nous proposons avant de voir la solution.

Essayez de découvrir la lettre que cette série continue:

E f h k ñ ?

La résolution de cette série n'est pas aussi évidente que dans le cas précédent, donc le moyen le plus simple de procéder est d'obtenir la série de nombres de base.

En utilisant le tableau que nous avons mentionné avant d'obtenir cette série de nombres de base:

5 6 8 11 15 ?

Si nous ne voyons pas le facteur de série clair, il est préférable de calculer les augmentations entre les deux termes de la série:

5     (+1)     6     (+2)     8     (+3)     onze     (+4)     quinze           ?

Si nous regardons l'augmentation, nous voyons que nous avons une série qui augmente d'une unité entre deux termes, donc la prochaine augmentation sera (+5).

Donc, Le prochain élément de la série de base sera de 15 + 5 = 20 Et si nous regardons dans le tableau d'équivalence, nous verrons que la position 20 de l'alphabet occupe la lettre "S", Donc ce sera la réponse.

Maintenant, complimons-le un peu plus. Trouvez les paroles qui continuent cette série:

Ou h d b ?

Dans ce cas, nous avons une série décroissante. La façon la plus simple de procéder est, encore une fois, d'obtenir la série de numéros de base:

16 8 4 2 ?

Nous obtenons les augmentations entre les deux termes:

16     (-8)      8      (-4)       4      (-2)       2             ?

Dans ce cas, nous n'avons pas de facteur fixe, il pourrait donc s'agir d'une série arithmétique de facteur variable ou d'une série géométrique.

Voyons s'il s'agit d'une série géométrique obtenant le facteur multiplicateur (ou diviseur) entre tous les deux termes de la série de base qui est: (÷ 2)

Nous avons une série arithmétique dans laquelle chaque élément est calculé en divisant le précédent par 2, donc L'élément suivant de la série de base sera: 2 ÷ 2 = 1 et la lettre qui occupe cette position dans l'alphabet est le "A".

Voyons un dernier exemple avant de passer à la section suivante:

J S C M V ?

Cette affaire est quelque chose de déconcertant puisque nous avons l'une des lettres du principe de l'alphabet, le "C", au milieu de la série, et des deux côtés, il a des lettres qui sont positionnées plus tard par ordre alphabétique, donc, à première vue , non, il est clair s'il s'agit d'une série croissante ou décroissante.

Nous procéderons de la manière habituelle, nous allons donc calculer la série de nombres de base:

10 20 3 13 23 ?

Ici, les augmentations de la série de bases ne nous donnent pas un facteur clair:

dix     (+10)      vingt     (-17)      3      (+10)       13     (+10)      23           ?

Dans ce cas, nous devons nous rappeler que l'alphabet a une séquence cyclique lors de la résolution de la série. C'est-à-dire que la prochaine lettre après le "z" sera le "A" qui occuperait la position "28".

Puisque nous voyons que le facteur (+10) apparaît plusieurs fois, nous vérifierons si la lettre "C" est une (+10) positions de la lettre "S" et nous voyons effectivement que c'est le cas.

Du "S" au "Z" puis du "A" au "C", il y a un total de 10 positions, donc, en ajoutant (+10) au numéro 20, nous dépassons la longueur de l'alphabet donc Ce que nous devons soustraire 27 (qui est le nombre de lettres d'alphabet) pour obtenir à nouveau la position valide d'une lettre.

Dans ce cas, 20 + 10 - 27 = 3, ce qui correspond à la lettre "C". Avec cela, nous avons montré que le facteur de série est (+10), donc si nous l'ajoutons au dernier élément de la série de base, nous aurons 23 + 10 = 33 et si nous soustrayons 27, nous obtiendrons 6, ce qui est la position de le Lettre "f".

Avec ces exemples, vous pouvez clairement voir le moyen de résoudre ce type de série.

Si nous comptons sur le tableau d'équivalence, nous pouvons transformer n'importe quelle série alphabétique en une série numérique et résoudre ceci avec tout ce qui est appris dans la vidéo de la série numérique.

Multiples séries d'alphabétisation entrecoupées

Comme dans la série numérique, il est possible de trouver deux séries ou plus en un seul. Ce type de série est facile à détecter car la longueur de la série sera plus grande.

Une fois que nous aurons conclu que nous sommes confrontés à deux séries entrecoupées, nous allons ne résoudre que la série qui affecte la solution. Voyons quelques exemples:

C z D Z F Z G Z I Z J Z L Z ?

Ici, nous voyons que le "z" est répété entre deux lettres, nous aurons donc deux séries entrecoupées. Un très simple dans lequel la même lettre apparaît toujours et cet autre:

C D F G I J L ?

Lors du calcul de la série de base, nous obtenons ce qui suit:

C    (+1)   D   (+2)  F  (+1)    g   (+2)    Toi   (+1)    J    (+2)     L         ?

Les augmentations sont alternativement (+1) et (+2), donc l'augmentation suivante sera (+1) et La lettre qu'ils nous demandent est donc le "M".

Dans ce cas, l'une des séries avait toutes ses termes égaux, (la lettre "z"), mais ils ne le rendront pas toujours aussi facile. Regardons un dernier exemple plus compliqué:

T d s e r g q j p n o ?

La longueur de la série nous fait déjà soupçonner que deux séries entrecoupées peuvent être traitées, nous les séparons donc pour essayer de les résoudre:

1 série: t s r q p o
Série 2: D E G J N            ?

Puisque la valeur qu'ils demandent correspond à la série 2, nous pouvons oublier la première série (bien qu'il semble qu'il s'agisse d'une simple série décroissante avec le facteur 1).

Nous calculons la série de base de la seconde, et son augmentation, et obtenons ceci:

4   (+1)   5    (+2)     7     (+3)    dix    (+4)    14          ?

Le saut entre toutes les deux valeurs de la série augmente en une unité, donc l'augmentation suivante sera (+5) et la base suivante de la série de base sera de 14 + 5 = 19 qui correspond au Lettre r ".

Bien que ce ne soit généralement pas très courant, Nous pourrions rencontrer jusqu'à trois séries entrecoupées. Ce sera la longueur de la série qui nous donnera des indices sur le fait qu'il s'agit d'une série multiple ou non.

Série numérique dans les tests psychotechniques, comment les surmonter

Séries mixtes

Les séries mixtes sont formées par des séries numériques et alphabétiques mixtes. Ce serait un cas spécifique de la section précédente dans laquelle l'une des séries n'est pas alphabétique.

La procédure pour les résoudre serait la même que nous expliquons avant. Dans ce cas, il sera plus évident que nous sommes devant deux séries entrelacées.

Regardons un exemple:

S 45 x 28 C 11 h 21 m ? Q

Ici, nous trouvons plusieurs surprises. La première est que la valeur qu'ils demandent n'est pas la dernière position.

Cela peut arriver et ne devrait pas s'inquiéter. La procédure à suivre a déjà été vue dans le Vidéo de la série numérique.

Ce qui est inquiétant, c'est que la série numérique n'est pas où la prendre, et malheureusement la valeur qu'ils nous demandent est précisément ce sous-série sous-série.

Les valeurs numériques augmentent et diminuent sans aucun critère clair, donc après quelques minutes de frustration en essayant de résoudre la série, nous verrons si les deux sont interdépendants, c'est-à-dire que les valeurs de l'une dépendent de l'autre.

Compte tenu de la nature cyclique de la série alphabétique, il est possible que la série numérique soit basée sur les positions des lettres autour et devient également une série cyclique.

Pour le vérifier, nous remplacerons les valeurs de chaque lettre par sa position dans l'alphabet et prierons pour l'inspiration pour arriver:

20 45 25 28 3 11 8 21 13   ?   18

Ici, nous voyons que les valeurs de la série numérique se développent et diminuent à mesure que les valeurs de la série alphabétique le font, c'est donc une question de temps que nous concluons que les valeurs de la série numérique sont calculées en ajoutant Les valeurs de la série alphabétique autour de lui: 45 = 20 + 25, 28 = 25 + 3, 11 = 3 + 8, 21 = 8 + 13 et donc Le terme recherché sera de 13 + 18 = 31.

Cela nous donne une idée de la variété des déclarations de série qui peuvent nous élever.

La seule façon de surmonter avec succès tout problème de ce type est basée sur la pratique de tout ce qui est possible Ces types d'exercices pour pouvoir reconnaître rapidement chaque cas et ne pas perdre autant de temps pendant les tests réels.

Modifications et variations

Nous avons déjà vu comment résoudre la série de base, qui est généralement la majorité de ceux que nous trouverons.

Sur ces séries, les examinateurs ajoutent parfois des modifications qui affectent également le résultat.

Ces modifications sont généralement basées sur la répétition des éléments d'une série, la distinction entre les voyelles et les consonnes, l'utilisation de majuscules et de minuscules, de séries de bloc.

Voyons quelques exemples:

M n n p q s t t ?

Si nous avons déjà une pratique avec la série d'alphabétisation, nous pouvons résoudre la plupart d'entre eux sans recourir à calculer la série de bases.

Dans ce cas, nous voyons clairement une série alphabétique ascendante dans laquelle une valeur sur deux est répétée.

Il est également observé que lorsqu'une lettre est répétée, une position est sautée dans l'alphabet, donc La valeur suivante sera "V".

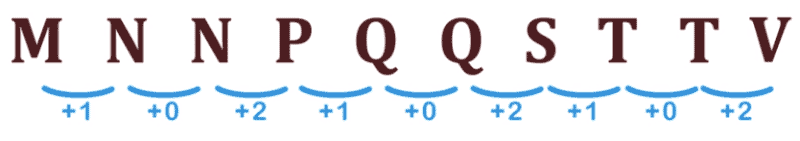
Regardons un autre cas:

Ou e u i a ?

Dans cet exemple, nous observons clairement qu'ils alternent et les minuscules et que les voyelles sont utilisées uniquement.

C'est une série descendante avec un saut d'une lettre entre deux termes de la série.

Puisque c'est une série cyclique, La prochaine lettre sera une minuscule "ou".

Il pourrait également être considéré comme une série cyclique ascendante avec un facteur +3 et la solution serait exactement la même.

Regardons un dernier exemple dans cette section:

1AAZ B2BY CC3X ?

Dans ce cas, nous avons une série alphabétique en blocs qui mélangent les nombres et les lettres. Une vraie gallimaties.

Ici, nous devons essayer de rechercher la logique des termes de la succession en voyant les directives suivantes.

D'une part, nous voyons que dans chaque bloc, un seul nombre apparaît, ce qui augmente à chaque terme et qui est déplacé vers la droite coïncidant avec la position qu'elle occupe à l'intérieur du bloc.

Étant donné que tous les termes ont la même longueur de 4 caractères, nous pouvons déduire cela Le terme recherché ressemblera à ceci: ???4.

Nous pouvons également observer que dans chaque bloc, nous avons une lettre qui est répétée, qui progresse dans l'ordre alphabétique et qui est toujours à gauche de l'autre lettre, donc La solution doit regarder: DD?4

Et enfin, nous voyons que la lettre que nous manquons de progrès dans l'ordre alphabétique descendant, donc Le bloc recherché sera: DDW4.

Série littérale

Les séries littérales sont basées sur des mots individuels ou des ensembles de mots qui suivent un ordre logique. À partir de ces mots, l'initiale utilisée pour construire la série est normalement prise.

Voyons quelques exemples qui le rendront plus clair. Imaginez qu'ils proposent cette série:

U d t c c s o ?

Puisqu'il s'agit d'une série assez longue, et qu'elle ne semble suivre aucun modèle dans son ensemble, nous pourrions penser que ce sont deux séries entrecoupées, mais après plusieurs minutes d'efforts infructueux, nous devrons élever d'autres alternatives.

Dans ce cas, la traite d'une série alphabétique littérale formée par les initiales d'un ensemble de mots largement reconnaissables et qui suivent un ordre.

Devinez quels sont ces mots? Ceci est la solution:

OUNon   Dtoi   Tbœuf   Cuatro   CInc   SEIS   Siete   SOITChou   ?

Maintenant c'est beaucoup plus clair, juste? Le prochain élément de cet ensemble de mots serait "neuf" et donc la prochaine lettre de la série serait "N".

Nous proposons d'autres exemples typiques, ainsi que votre solution, mais vous devez garder à l'esprit que tout ensemble de mots qui suivent un ordre établi peut être un bon candidat pour ce type de série.

L M J V ?

Dans ce cas, il s'agit des jours de la semaine lundi, mardi, mercredi, jeudi, vendredi et Le prochain élément sera samedi, donc la solution de la série sera "S".

Essayons une autre série:

E f m a m J ?

Avez-vous résolu? En effet, ce sont les mois de l'année: janvier, février, mars, avril, mai, juin, donc La lettre regardée est le "J" de juin.

Et un dernier cas de ce type:

P s t c q ?

Qui correspondraient aux nombres ordinaux: première, deuxième, troisième, quatrième, cinquième et le terme que nous recherchons, sera Le "S" sixième.

Dans ces types de problèmes, il est également possible que vous trouviez une série qui représente un ensemble de mots ordonnés par inverse, c'est-à-dire que la première série de cette section deviendrait ceci:

N O S S C C T D ?

Voyons maintenant avec un autre exemple différent. Essayez de résoudre cette autre série:

? T e b a f l a

En plus des séries basées sur des ensembles de mots ordonnés, nous pouvons en trouver d'autres qui sont basés sur un seul mot.

Ils représentent généralement le mot écrit à l'envers, bien qu'il soit également possible de trouver leurs paroles désordonnées. Dans ce cas, si nous investissons l'ordre de la série, nous avons: a l f a b e t ?

La solution serait donc la lettre "ou" pour former le mot "alphabet".

Un autre ensemble de lettres largement utilisées dans la série alphabétique est celle du chiffres romains: I, V, X, L, C, D, M.

Test HTP, qu'est-ce que votre objectif et vos clés pour l'interpréter

Cas spéciaux

Si vous pensiez que nous avions déjà vu tous les types de séries alphabétiques existantes, vous avez très tort.

Comme nous l'avons déjà commenté sur le Vidéo de la série numérique, L'imagination des examinateurs peut créer la série la plus diversifiée, vous devez donc avoir un esprit ouvert lorsque vous essayez de les résoudre.

Selon le niveau académique des participants au test, vous pouvez trouver des séries basées sur l'ordre des nombres premiers, en puissances de nombres, dans la série Fibonacci, etc.

Donc, si une série résiste, il est probable qu'elle ne soit pas simplement basée sur l'ordre numérique des lettres de l'alphabet et que vous devrez rechercher des méthodes de résolution alternatives.

Donc, enfin, nous proposons une dernière série pour serrer les neurones.Chance!

A a c e i m m s t ?

La vérité est que c'est un exemple assez compliqué. Après avoir essayé en tant que série multiple, ensemble de mots ordonné et froissé plusieurs feuilles de papier, nous verrons quelles informations nous pouvons extraire de la série.

Nous pouvons voir que les lettres apparaissent dans l'ordre alphabétique, mais nous ne pouvons pas trouver de séquence, ou avec des nombres premiers, ou avec Fibonacci, ou avec des mots connus, ou avec les éléments du tableau périodique, ... afin que nous puissions penser que l'on pense que c'est un ensemble de lettres qui ont un sens dans son ensemble, c'est-à-dire, C'est un mot.

Étant donné que le mot n'est pas écrit à droite ou à l'envers, nous concluons que leurs lettres ont été arrière et comment? Eh bien, dans l'ordre alphabétique!

Alors maintenant "seulement" nous devons trouver un mot qui contient toutes les lettres de la série, y compris les paroles que nous devons découvrir. À moins que nous ayons une inspiration divine, après plusieurs tentatives de rejoindre des couples de lettres consonnes-vocales sous toutes les formes imaginables, Nous obtenons le mot matma?ICA, Nous allons donc réaliser que Les paroles de Look sont le "T".

La bonne nouvelle est qu'il est peu probable que vous trouviez une série aussi compliquée dans le Tests psychotechniques, Et vous savez que dans tous les cas, il est conseillé de laisser ceux qui vous sont les plus difficiles pour la fin.

Vous avez également cette entrée vidéo disponible:

Bonne chance dans vos oppositions!

Test pour Pratique pour les oppositions